Le persone che viaggiano in Australia dovranno ora autoisolarsi per 14 giorni, una delle misure annunciate nel fine settimana dal primo ministro Scott Morrison, con l’obiettivo di rallentare la diffusione del coronavirus e alleviare lo stress sui letti d’Ospedale.
Questo concetto generale di rallentamento della diffusione del virus è stato definito “appiattire la curva” dagli epidemiologi, esperti che studiano la frequenza con cui si verificano malattie in diverse popolazioni e perché. Il termine è diventato molto diffuso sui social media poiché le persone sono incoraggiate a praticare il “distanziamento sociale”. Ma in che modo il distanziamento sociale aiuta ad appiattire la curva? Possiamo spiegarlo facendo riferimento a ciò che i matematici chiamano “crescita esponenziale”.
Crescita esponenziale
Nelle prime fasi di un’epidemia, quando la maggior parte delle persone è suscettibile alle infezioni, i matematici possono modellare la diffusione di una malattia da persona a persona come essenzialmente un “processo di ramificazione” casuale. Se una persona infetta in media ne infetta altre due, il numero di persone infette raddoppia. Questo concetto è noto come crescita esponenziale. Ci sono molti fattori che influenzano la probabilità di infezione. In una pandemia, il tasso di crescita dipende dal numero medio di persone che una persona può infettare e dal tempo impiegato da quelle persone per diventare infettive.
La ricerca suggerisce che il numero di casi confermati di COVID-19 sta crescendo esponenzialmente in tutto il mondo con il numero che raddoppia ogni sei giorni circa.
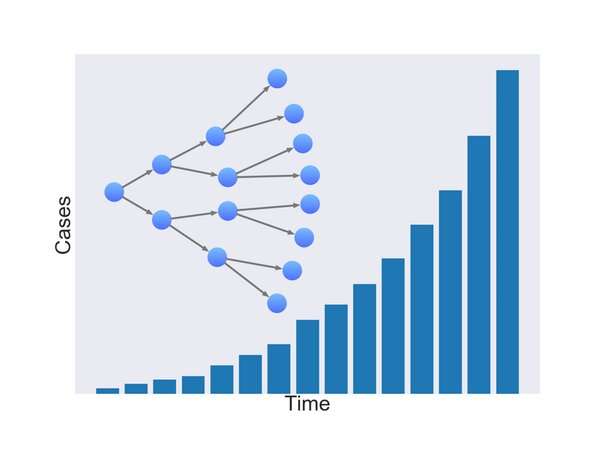
I modelli di crescita esponenziale si avvicinano strettamente alla realtà quando iniziano con un piccolo numero di individui infetti in una vasta popolazione, come quando il virus è emerso per la prima volta a Wuhan o quando è arrivato in Italia o in Iran. Ma non è un buon modello una volta che un gran numero di persone sono state infettate. Questo perché diminuisce la possibilità che una persona infetta contatta una persona sensibile, semplicemente perché ci sono meno persone sensibili in circolazione e una parte crescente di persone ha recuperato e sviluppato un certo livello di immunità.
Vedi anche: Quando e come usare la mascherina per proteggersi dal virus SARS-CoV-2?
Alla fine, le probabilità che una persona infetta contatta una persona sensibile diventa abbastanza bassa tanto da ridurre il tasso di infezione, portando a un minor numero di casi e, infine, alla fine della diffusione virale.
Appiattire la curva
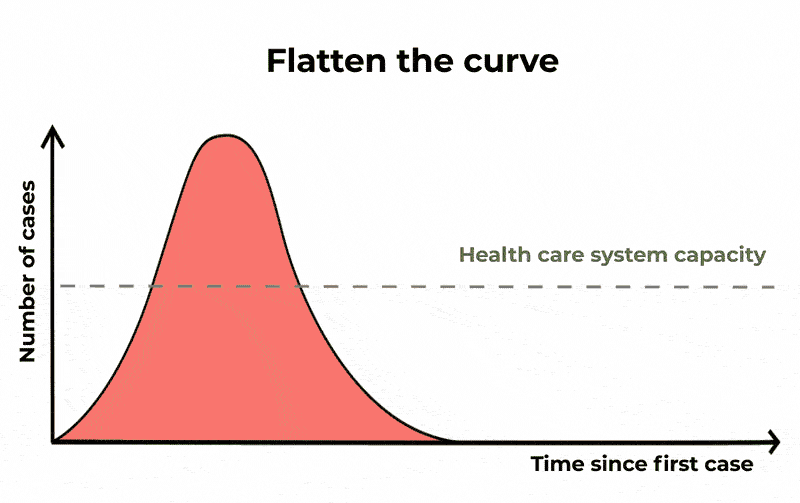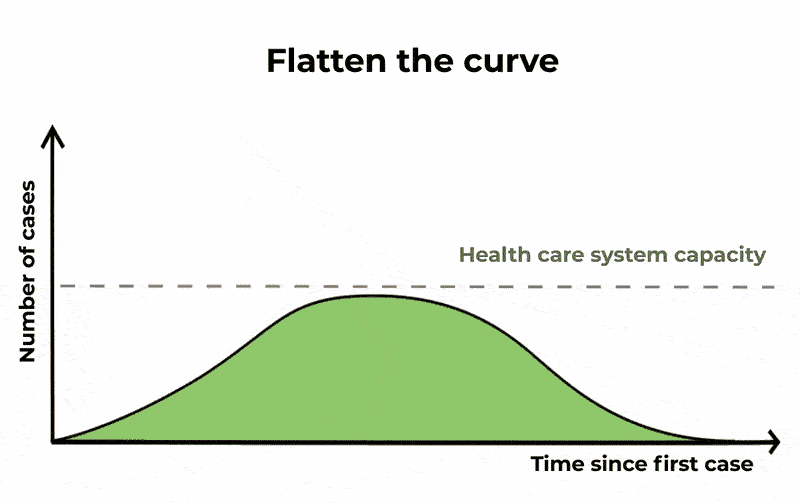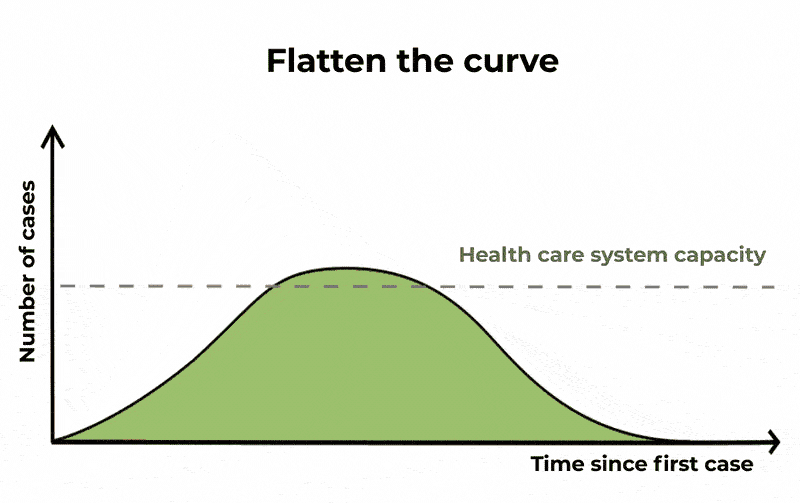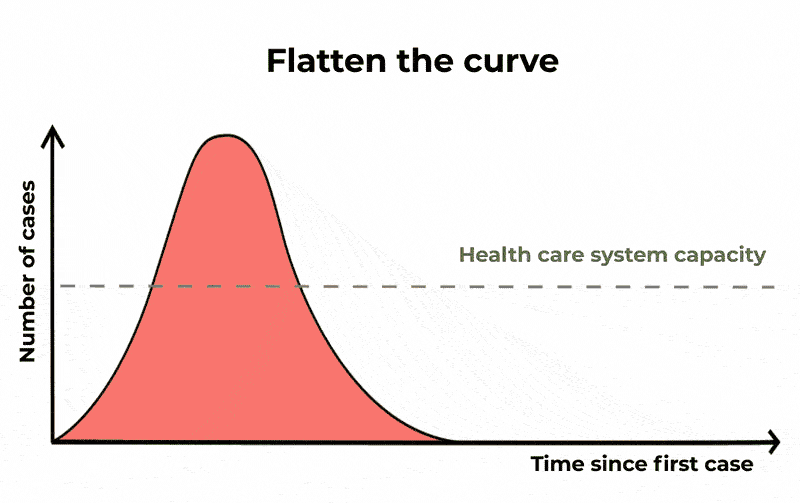
Le autorità sanitarie di tutto il mondo non sono state in grado di prevenire completamente la diffusione di COVID-19. Se i casi raddoppiano ogni sei giorni, in particolare gli Ospedali e le Unità di Terapia intensiva (ICU) saranno rapidamente sopraffatti, lasciando i pazienti senza le cure necessarie. Ma il tasso di crescita può essere rallentato riducendo il numero medio di casi a cui un singolo caso dà origine. In tal modo, lo stesso numero di persone sarà probabilmente infetto e l’epidemia durerà più a lungo, ma il numero di casi gravi verrà distribuito. Ciò significa che se si traccia un grafico del numero di casi nel tempo, la curva di salita e di discesa è più lunga, ma il suo picco è inferiore. “Appiattendo la curva” in questo modo, le ICU avranno meno probabilità di esaurire la loro capacità. Poiché attualmente non esiste un vaccino o un farmaco specifico per COVID-19, l’unico modo per ridurre la trasmissione è attraverso una buona igiene, isolando i casi sospetti e misure di allontanamento sociale come la cancellazione di eventi di grandi dimensioni e la chiusura delle scuole.
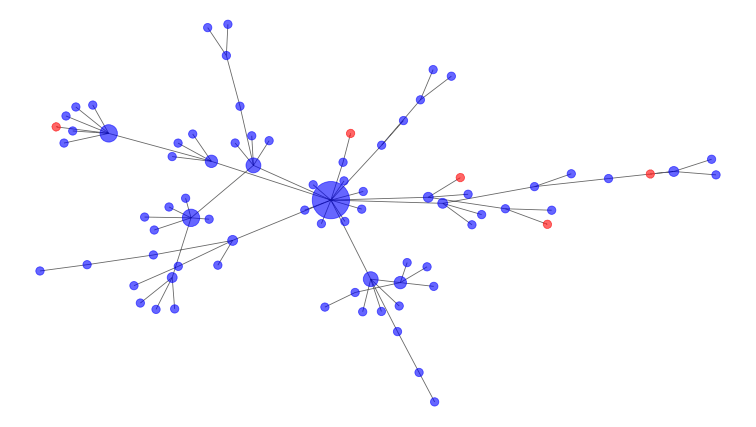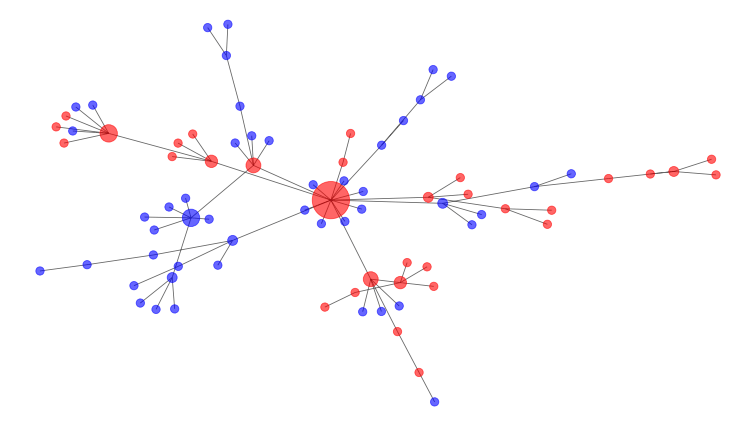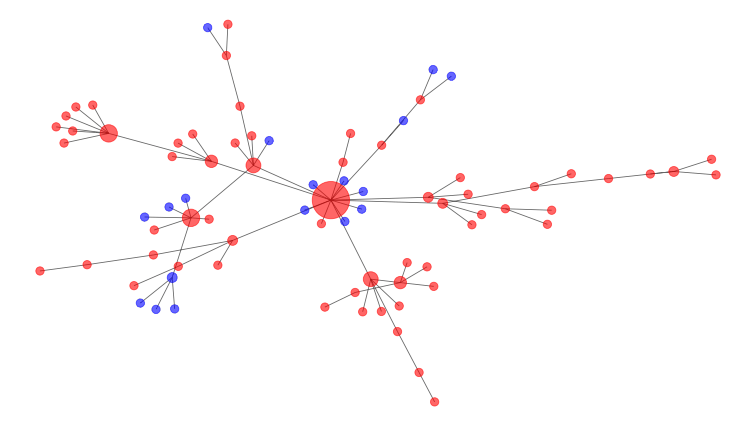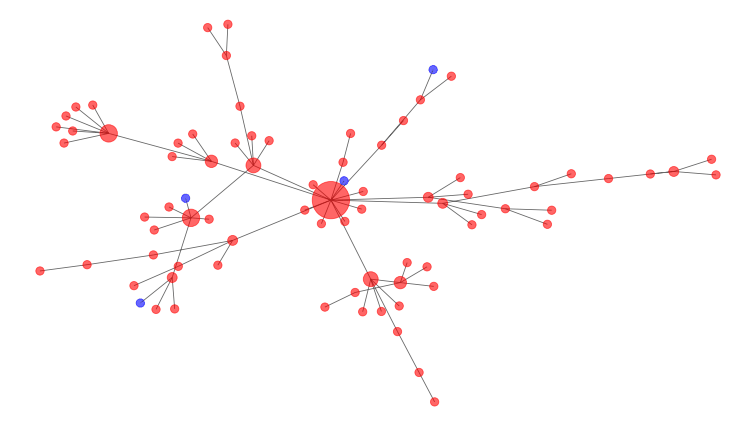
Questo grafico mostra come un’epidemia potrebbe diffondersi nel tempo attraverso una rete. I punti blu sono soggetti sensibili, mentre i punti rossi sono persone infette. Due punti sono collegati da una linea se sono in contatto tra loro, e più contatti ha una persona, più grande è il suo punto sulla rete.
Evita i super-spargitori
Naturalmente, la situazione non è così semplice come un semplice processo di ramificazione. Alcune persone interagiscono più di altre e potrebbero entrare in contatto con molti gruppi diversi. I matematici modellano queste connessioni come un social network, come quello qui riportato. Le persone infette sono nodi rossi e le persone sensibili sono blu. Il grande nodo al centro del diagramma è un super-spargitore, una persona che si collega a molti altri e quindi ha più potenziale per diffondere la malattia. Gli interventi aiutano a rimuovere i nodi e a interrompere le connessioni. Nel diagramma sopra, il nodo centrale grande e altamente connesso sarebbe il migliore da rimuovere per interrompere le connessioni. Ecco perché è una buona idea evitare grandi raduni pubblici durante l’epidemia di COVID-19. Le simulazioni matematiche del distanziamento sociale hanno mostrato come spezzare la rete aiuta ad appiattire la curva dell’infezione.
Come la matematica aiuta
Quanta distanza sociale è necessaria per appiattire la curva abbastanza da evitare che gli Ospedali vengano sopraffatti? È sufficiente mettere in quarantena le persone che sono state in contatto con casi confermati? Abbiamo bisogno di una chiusura diffusa di eventi, scuole e luoghi di lavoro?
Siamo ancora nelle prime fasi dell’epidemia di COVID-19 e c’è una grande incertezza sulle caratteristiche di questo virus. Per prevedere con precisione la crescita di COVID-19, è necessario determinare le dinamiche sottostanti della trasmissione che sono guidate da fattori tra cui:
1)Quante persone in media infetta un individuo? (il “numero di riproduzione” che, secondo l’Organizzazione Mondiale della Sanità, è attualmente compreso tra 1,4 e 2,5 persone );
2)Quanto tempo trascorre prima dell’inizio dei sintomi? (il “periodo di incubazione”, stimato in 5,1 giorni);
3)Quale percentuale di trasmissione si verifica prima dell’inizio dei sintomi, se presente? Poiché tali dati verranno raccolti e integrati nei modelli successivamente, nei prossimi mesi saremo in una posizione migliore per offrire previsioni accurate sul corso di COVID-19.
Fonte: Medicalxpress

